A 3D triple negative metamaterial

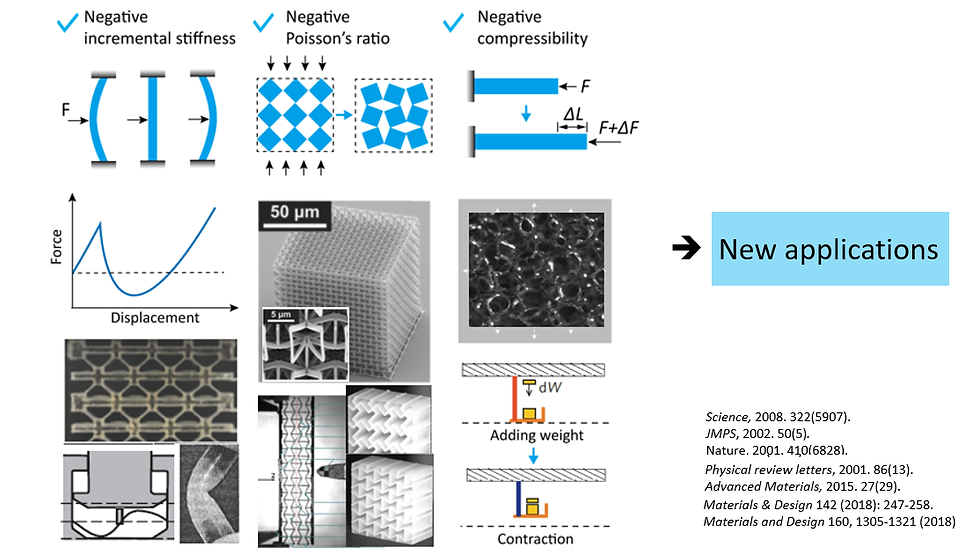
We've recently discovered a three-dimensional mechanical metamaterial that simultaneously possesses negative stiffness, negative bulk modulus, and negative Poisson’s ratio. This metamaterial is a periodic arrangement of binder-shell elements. Under compression, the spherical shells dent inwards which cause the material to contract in the lateral directions. Note that the spheres may bulge slightly but the Poisson's ratio is based on measurements of the outer surfaces of the multi- sphere specimen, thus the Poisson's ratio is negative.

The metamaterial achieves stiffness and Poisson’s ratio approaching negative infinity by harnessing snap-through instability.

At larger deformations, snap through instability occurs, exhibiting negative incremental stiffness. Interestingly, when "snap back" is found in the equilibrium path, the force will drop suddenly under displacement controlled loading. Such a "snap-back" instability leads to singularity in the incremental stiffness and incremental Poisson’s ratio, both approaching negative infinity.

Concepts and applications of metamaterials with negative material indices. Novel applications can be envisioned for a metamaterial possessing simutaneously negative stiffness, negative Poisson's ratio, and negative bulk modulus.

The incremental stiffness and Poisson’s ratio become the “applicable” stiffness and Poisson’s ratio when prestressed to the corresponding strain.

The negative bulk modulus is a byproduct of negative stiffness and negative Poisson’s ratio, making the metamaterial triple negative. Moreover, the metamaterial concept can be extended to other lattices and even 2D and non-periodic structures. Recent progress in techniques like self-assembling further enables the fabrication of the metamaterial at the nanoscale.

The significance of the proposed triple negative metamaterial has two folds:

1.Opening new possibilities to prevent deformation localization, thus fight premature failure.

2.Enabling the rational control over negative stiffness material, thus facilitate the application of homogeneous negative stiffness/compressibility materials.

For instance, in traditional materials, negative stiffness means softening, which typically leads to localized deformations which typically leads to failure. We found that the multi-negative index metamaterial can satisfy the strong ellipticity condition, therefore, deformations will be propagated to the whole material instead of being localized. This also means that a block of the metamaterial with many unit cells is stable under displacement-constraint.

We've found a negative stiffness material (softening) that satisfies the strong ellipticity condition, thus the material will deform globally in a consistent pattern, instead of forming localized bands.

Our study provides useful insights to the harness of instability and the design of multi-negative index materials.Potential applications of the metamaterial include that for auxetic materials, like mechanical diodes (an auxetic material stuck in a tube is easy to push in but hard to pull out) and composites with unbounded shear to bulk modulus [1] and high crashworthiness [2]. Special performances enabled by negative stiffness include high energy absorption [3] and composites with unbounded damping and stiffness [4-6]. Furthermore, negative compressive metamaterial brings applications like actuators, force amplifiers, and micromechanical controls [7].

In summary, the proposed triple negative material can provide multiple functions enabled by the three negative indices. Another important discovery we've found is that the triple negative performance satisfies strong ellipticity, thus provides a promising approach to prevent the formation of localized deformation bands thus premature failure. This results is publised in arXiv:1903.00523 (2019) [Preprint].

References:

[1] S. Xinchun and R. S. Lakes, Physica status solidi (b) 244, 1008 (2007).

[2] S. Hou, T. Li, Z. Jia, and L. Wang, Materials & Design 160, 1305 (2018).

[3] S. Shan, S. H. Kang, J. R. Raney, P. Wang, L. Fang, F. Candido, J. A. Lewis, and K. Bertoldi, Adv. Mater. 27, 4296 (2015).

[4] R. S. Lakes, T. Lee, A. Bersie, and Y. Wang, Nature 410, 565 (2001).

[5] R. Lakes, Philos. Mag. Lett. 81, 95 (2001).

[6] T. Jaglinski, D. Kochmann, D. Stone, and R. Lakes, Science 315, 620 (2007).

[7] Z. Chen, P. Zhan, Z. Wang, J. Zhang, W. Zhang, N. Ming, C. T. Chan, and P. Sheng, Adv. Mater. 16, 417 (2004).